curvas complexas Graceli

	K	dz z	=		20	logx/x[n] r e^it r e^it	dt = 2 *logx/x[n]

função complexa com as sequências Graceli.

f´[sG log d/d [n...]*p[n..]* [w/√ [n..]* ]* [sG y / √ [n...] ] *p[n..]*[w/√[n..] = df / d [sG log d/d [n...]*p[n..]* [w/√ [n..]* ]* [sG y / √ [n...] ] *p[n..]*[w/√[n..].

sistema multi matemático Graceli. onde temos numa mesma função diferenciais, integrais, matriz, estatística, e geometria oscilatória Graceli.

p= progressão.

p [n..]* [w/√ [n..]
[sG log d/d [n...]*p [n..]* ]* [sG y / √ [n...] ]
p[n..]* [w/√ [n..]

[sG log d/d [n...]*p[n..]* [w/√ [n..]* ]*  [sG y / √ [n...] ]

[sG log d/d [n...]*p[n..]* [w/√ [n..]* ]*  [sG y / √ [n...] ] *p[n..]*[w/√[n..]

exemplo para área de esferas.

* [sG log d/d [n...] ]*  [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R].

[sG log d/d [n...]*p[n..]* [w/√ [n..]* ]* [sG y / √ [n...] ] *p[n..]*[w/√[n..]

para cada sequência de log é multiplicável por uma sequência √ou todas.

no caso de uma temos ponto como se fosse uma tangente, e se for para todas temos uma integral.

e se for de todas de log, por todas de √, temos matrizes,e formas geométricassobre formas geométricas.

QUARTA-FEIRA, 28 DE MAIO DE 2014

e^{i\theta}=\cos\theta +i\mathrm{sen}\,\theta.

+ [sG log d/d [n...] ]* [ / ] [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

\lg z = \lg r +

i \lg e

(

\theta

2k\pi

) + [sG log d/d [n...] ]* [ / ] [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

$\ln z$ = $\ln r$ + $i$ ( $\theta$ ± $2k\pi$ ) + [sG log d/d [n...] ]* [ / ] [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

$e^{i\theta}=\cos\theta +i\mathrm{sen}\,\theta.$ + [sG log d/d [n...] ]* [ / ] [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

$\lg z = \lg r +$ $i \lg e$ ( $\theta$ ± $2k\pi$ )

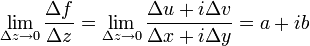\lim_{\Delta z \to 0} \frac {\Delta f}{\Delta z} = \lim_{\Delta z \to 0} \frac {\Delta u + i\Delta v}{\Delta x + i\Delta y} = a+ i b

+ [sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l

Com log,

√

, e ondas temos uma função que é composta de várias tangentes em cada curva da onda, em momentos e pontos diferentes e alturas diferentes.

E sem ondas temos uma curva com uma só concavidade. Ou seja, uma só curva.

E temos um sistema de pontos de cada sequência onde temos as diferenciais.

Mas, no conjunto de pontos temos as integrais.

Ou seja, é um sistema infinitesimal onde a própria função é diferencial e integral ao mesmo tempo.

Onde o importante é o caminho sequencial, e não o resultado final.

Logx/x [n...] ou [y] *[/] [+] [-]   h/

√

[n...]

Logx/x [n...] ou [y] *[/] [+] [-]   h/

√

[n...]* ondas [lambda].

Logx/x [n...] ou [y] *[/] [+] [-]   h/

√

[n...]* ondas [lambda] * [a, R, 0]

f´ [sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,+ $f'(z) =\frac {\part u}{\part x} + i \frac {\part v}{\part x} = \frac {\part v}{\part y}- i \frac {\part u}{\part y}$ .

+ [sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

ordem das sequencias Graceli.

a sequencia de logx/x [n...] determina que em cada divisão temos valores para aquela ordem sequencial divisória.

[sG log d/d [n...]

o mesmo acontece com as raízes quadrada e elevada a três [3], onde conforme se vai dividindo temos valores por ordem sequencial.

[sG y / √ [n...]

onde cada sequência multiplicável por todas as sequências sequintes temos as matrizes sequenciais Graceli.

geometria quântica sequencial Graceli.

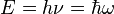E = h \nu = \hbar \omega

+ [sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

com geodésicas.

E = h \nu = \hbar \omega

G_{\mu\nu} = R_{\mu\nu} - {R \over 2} g_{\mu\nu} + \Lambda g_{\mu\nu} = {8 \pi G \over c^4} T_{\mu\nu}

+ [sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

E = h \nu = \hbar \omega

+ [sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

E = h \nu = \hbar \omega

G_{\mu\nu} = R_{\mu\nu} - {R \over 2} g_{\mu\nu} + \Lambda g_{\mu\nu} = {8 \pi G \over c^4} T_{\mu\nu}

+ [sG log d/d [n...] ]* [sG y / √ [n...] ]

\lambda

* [a R, 0 -R] * a,l, l,

geometria matrial Quântica Graceli.

[sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

all = altura, longitude, latitude.

{\int}

[sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

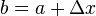b = a + \Delta x

+ [sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R] * a,l, l,

para fluxo de lados de triângulos ou retângulos.

esferas.

* [sG log d/d [n...] ]* [sG y / √ [n...] ] *

\lambda

* [a R, 0 -R].

para triângulos.

\alpha + \beta + \gamma = 180^\circ

+ [sG log d/d [n...] ]* [sG y / √ [n...] ] *cc* *

\lambda

* [a R, 0 -R].

cc = côncavo ou convexo.

\lambda

= ondas de lados

geometria oscilatória e matricial Graceli.

exemplo de geometria oscilatória Graceli para esferas.

* log d/d [n...] * [a R, 0 -R].

d = diâmetro.

a = alternância entre números reais positivos e negativos e zero.

  * log d/d [n...] * y / √ [n...] * [a R, 0 -R].

   * [sG log d/d [n...] ]*  [sG y / √ [n...] ]* [a R, 0 -R].

sG = sequência Graceli.

estas variáveis oscilatórias podem ser usadas para volumes, lados, catetos, hipotenusa, e outras formas como triângulos, retângulos, etc.

geometria matricial Graceli.

onde cada sequencia leva a um resultado em certos instante e valor conforme a sequência em questão.

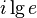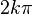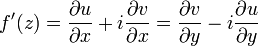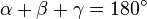* [sG log d/d [n...] ]*  [sG y / √ [n...] ]* [a R, 0 -R].

curvas complexas Graceli

domingo, 1 de junho de 2014

QUARTA-FEIRA, 28 DE MAIO DE 2014

Nenhum comentário:

Postar um comentário